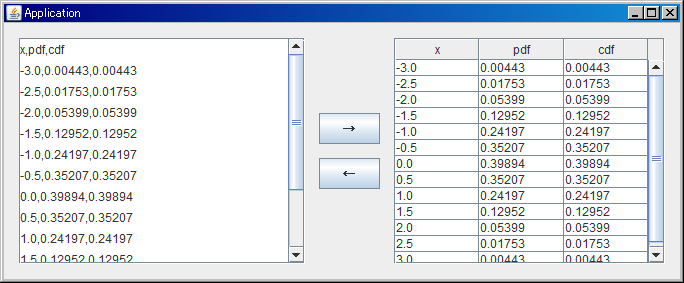
Java Swing でテキストエリア テーブルの例を作ってみました。
csv っぽい形式で JTextArea 入力されているデータを JTable に読み込んだり、JTable のデータを csv っぽい形式に掃き出す事ができます。
ポイント
最初に作成した JTable クラス型のオブジェクト tableFirst に new JTable(data) 等を代入しても、テーブルの更新ができません。
// not work JTable tableFirst = new JTable(datamatrixFirst, colnameFirst); tableFirst = new JTable(datamatrixSecond, colnameSecond);
TableModel クラス型のオブジェクト tableModel で初期化し、tableModel の方を setDataVector メソッドで編集してあげると、テーブルがちゃんと更新されます。
// work DefaultTableModel tableModel = new DefaultTableModel(datamatrixFirst, colnameFirst); JTable tableFirst = new JTable(tableModel); tableModel.setDataVector(datamatrixSecond, colnameSecond);
ソースコード
import javax.swing.JTextArea; import javax.swing.SwingUtilities; import javax.swing.JPanel; import javax.swing.JFrame; import javax.swing.JTable; import java.awt.Rectangle; import java.io.BufferedReader; import java.io.IOException; import java.io.StringReader; import java.util.ArrayList; import javax.swing.JScrollPane; import javax.swing.table.DefaultTableModel; import javax.swing.JButton; public class myTable { /** * @param args */ public static void main(String[] args) { SwingUtilities.invokeLater(new Runnable() { @Override public void run() { myTable application = new myTable(); application.getJFrame().setVisible(true); } }); } private String[] colName = {"x", "pdf", "cdf"}; private Double[][] dataMatrix = { { -3.0, 0.00443, 0.00443}, { -2.5, 0.01753, 0.01753}, { -2.0, 0.05399, 0.05399}, { -1.5, 0.12952, 0.12952}, { -1.0, 0.24197, 0.24197}, { -0.5, 0.35207, 0.35207}, { 0.0, 0.39894, 0.39894}, { 0.5, 0.35207, 0.35207}, { 1.0, 0.24197, 0.24197}, { 1.5, 0.12952, 0.12952}, { 2.0, 0.05399, 0.05399}, { 2.5, 0.01753, 0.01753}, { 3.0, 0.00443, 0.00443} }; private JTable dataTable = null; private JButton jButtonTable2Text = null; private JButton jButtonText2Table = null; private JPanel jContentPane = null; private JFrame jFrame = null; private JScrollPane jScrollPane = null; private JScrollPane jScrollPaneTextArea = null; public DefaultTableModel tableModel = new DefaultTableModel(dataMatrix, colName); public JTextArea tableText = null; /** * This method initializes dataTable * * @return javax.swing.JTable */ private JTable getDataTable() { if (dataTable == null) { dataTable = new JTable(tableModel); } return dataTable; } /** * This method initializes jButtonTable2Text * * @return javax.swing.JButton */ private JButton getJButtonTable2Text() { if (jButtonTable2Text == null) { jButtonTable2Text = new JButton(); jButtonTable2Text.setBounds(new Rectangle(315, 135, 61, 31)); jButtonTable2Text.setText("←"); jButtonTable2Text.addActionListener(new java.awt.event.ActionListener() { @Override public void actionPerformed(java.awt.event.ActionEvent e) { textUpdate(); } }); } return jButtonTable2Text; } /** * This method initializes jButtonText2Table * * @return javax.swing.JButton */ private JButton getJButtonText2Table() { if (jButtonText2Table == null) { jButtonText2Table = new JButton(); jButtonText2Table.setBounds(new Rectangle(315, 90, 61, 31)); jButtonText2Table.setText("→"); jButtonText2Table.addActionListener(new java.awt.event.ActionListener() { @Override public void actionPerformed(java.awt.event.ActionEvent e) { tableUpdate(); } }); } return jButtonText2Table; } /** * This method initializes jContentPane * * @return javax.swing.JPanel */ private JPanel getJContentPane() { if (jContentPane == null) { jContentPane = new JPanel(); jContentPane.setLayout(null); jContentPane.add(getJScrollPane(), null); jContentPane.add(getJButtonText2Table(), null); jContentPane.add(getJButtonTable2Text(), null); jContentPane.add(getJScrollPaneTextArea(), null); textUpdate(); } return jContentPane; } /** * This method initializes jFrame * * @return javax.swing.JFrame */ private JFrame getJFrame() { if (jFrame == null) { jFrame = new JFrame(); jFrame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); jFrame.setSize(684, 283); jFrame.setContentPane(getJContentPane()); jFrame.setTitle("Application"); } return jFrame; } /** * This method initializes jScrollPane * * @return javax.swing.JScrollPane */ private JScrollPane getJScrollPane() { if (jScrollPane == null) { jScrollPane = new JScrollPane(); jScrollPane.setBounds(new Rectangle(390, 15, 271, 226)); jScrollPane.setViewportView(getDataTable()); } return jScrollPane; } /** * This method initializes jScrollPaneTextArea * * @return javax.swing.JScrollPane */ private JScrollPane getJScrollPaneTextArea() { if (jScrollPaneTextArea == null) { jScrollPaneTextArea = new JScrollPane(); jScrollPaneTextArea.setBounds(new Rectangle(15, 15, 286, 226)); jScrollPaneTextArea.setViewportView(getTableText()); } return jScrollPaneTextArea; } /** * This method initializes tableText * * @return javax.swing.tableText */ private JTextArea getTableText() { if (tableText == null) { tableText = new JTextArea(); } return tableText; } private void tableUpdate() { BufferedReader textInput = new BufferedReader(new StringReader( tableText.getText() )); ArrayList<String[]> list = new ArrayList<String[]>(); String line = null; String[] arrayline = null; try { while ((line = textInput.readLine()) != null) { arrayline = line.split(","); list.add(arrayline); } textInput.close(); String[] colName = list.get(0); list.remove(0); String[][] dataMatrix = list.toArray(new String[0][0]); tableModel.setDataVector(dataMatrix, colName); } catch (IOException e) { } } private void textUpdate() { String textUpdated = ""; for (int j = 0; j < tableModel.getColumnCount(); j++) { if (j != tableModel.getColumnCount() - 1) { textUpdated = textUpdated + tableModel.getColumnName(j) + ","; } else { textUpdated = textUpdated + tableModel.getColumnName(j) + "\n"; } } for (int i = 0; i < tableModel.getRowCount(); i++) { for (int j = 0; j < tableModel.getColumnCount(); j++) { if (j != tableModel.getColumnCount() - 1) { textUpdated = textUpdated + tableModel.getValueAt(i, j) + ","; } else { textUpdated = textUpdated + tableModel.getValueAt(i, j) + "\n"; } } } tableText.setText(textUpdated); } }